Cayley-Bacharach theorem

Introduction
Theorems by Pascal and Pappus
Associativity of the group law on a cubic curve
- Group law on a cubic curve
- Associativity from Cayley-Bacharach
References

Introduction

Statement of the theorem

The Cayley-Bacharach theorem says the following:

Let \(C_1\) and \(C_2\) be two cubic curves in \(\mathbb{P}^2\) that intersect in nine distinct points. Let \(D\) be a cubic curve in \(\mathbb{P}^2\) that passes through eight of these points. Then \(D\) also passes through the the ninth intersection point.

A nice overview about the history of this theorem and related results can be found in this paper by Eisenbud, Green and Harris.

Cubic curves in the plane

A cubic curve \(C\) in the plane is given by an equation

\begin{align} F(x_0, x_1, x_2) = a x_0^3 + b x_1^3 + c x_2^3 + d x_0^2 x_1 + e x_0^2 x_2 + f x_0 x_1^2 + g x_1^2 x_2 + h x_0 x_2^2 + i x_1 x_2^2 + j x_0 x_1 x_2 = 0. \label{eq:general-cubic} \end{align}

The coefficients \((a, b, \ldots, j)\) completely determine the curve \(C\). However, as the equation is homogeneous, so we can multiply it by a constant \(\lambda\) without changing the curve \(C\). Therefore two tuples of coefficients \((a, b, \ldots, j)\) and \((a', b', \ldots, j')\) that are related by a rescaling determine the same curve. This shows that the space of all cubic curves in the plane is a nine-dimensional projective space \(\mathbb{P}^9\) with homogeneous coordinates \([a : b : \ldots : j]\).

Consider the situation where a point \(P \in \mathbb{P}^2\) is given and we want to study the space of all cubics in the plane that pass through \(P = [p_0 : p_1 : p_2]\). Every cubic (given by an equation \(F = 0\)) passing through \(P\) has to satisfy \(F(p_0, p_1, p_2) = 0\). From equation \eqref{eq:general-cubic} we see that this imposes one linear condition on the coefficients \([a : b : \ldots : j]\), so the space of cubics passing through \(P\) is a hyperplane in \(\mathbb{P}^9\).

Demanding that a cubic passes through more points, we obtain more linear conditions that the coefficients in \eqref{eq:general-cubic} have to satisfy. If we ask for cubics passing through nine prescribed points, there are nine conditions imposed on the nine-dimensional space \(\mathbb{P^9}\). If the conditions are all independent (corresponding to the prescribed points being in general position), there is a unique solution for the coefficients \([a : b : \cdots : j]\). Thus, nine general points in the plane determine a cubic.

Sketch of the proof

Now we can look at the situation in the theorem, where nine distinct points \(P_1, \ldots, P_9\) are given as the intersection of two cubics

\begin{align} C_1: F_1(x_0, x_1, x_2) = 0, \qquad C_2: F_2(x_0, x_1, x_2) = 0. \end{align}

We pick any eight of them, \(P_1, \ldots, P_8\), and study the space of cubics passing through all of them. This imposes eight (independent) linear conditions on the coefficients \([a : b : \ldots : j]\). As \(\mathbb{P}^9\) is nine-dimensional, the solution space is one-dimensional and is spanned by linear combinations of the form

\begin{align} \lambda_1 [a_1 : b_1 : \cdots : j_1] + \lambda_2 [a_2 : b_2 : \cdots : j_2], \quad [\lambda_1 : \lambda_2] \in \mathbb{P}^1, \label{eq:linear-combinations} \end{align}

where \([a_1 : b_1 : \cdots : j_1]\) and \([a_2 : b_2 : \cdots : j_2]\) are the coefficients corresponding to \(F_1\) and \(F_2\) respectively. The polynomial corresponding to the linear combinations \eqref{eq:linear-combinations} defines a curve \(D\) that passes through the points \(P_1, \ldots, P_8\),

\begin{align} D: G(x_0, x_1, x_2) = \lambda_1 F_1(x_0, x_1, x_2) + \lambda_2 F_2(x_0, x_1, x_2) = 0, \quad [\lambda_1 : \lambda_2] \in \mathbb{P}^1. \end{align}

We can now check what happens for the ninth point: Since \(F_1(P_9) = F_2(P_9) = 0\), we immediately get \(G(P_9) = 0\), so the curve \(D\) also passes through \(P_9\).

Generalizations to higher degrees

The theorem can be generalized to higher degree curves as follows.

Let \(C_1\) and \(C_2\) be two curves in \(\mathbb{P}^2\) of degrees \(d_1\) and \(d_2\) respectively that meet in \(d_1 d_2\) distinct points. Let \(D\) be a curve in \(\mathbb{P}^2\) of degree \(d_1 + d_2 - 3\) that passes through \(d_1 d_2 - 1\) of these points. Then \(D\) also passes through the last intersection point.

The classical case described above is obtained for \(d_1 = d_2 = 3\) which is also the first "interesting" case in the sense that for lower degrees the statement is trivial. A proof of the more general case can be found in Chapter 5.2 of Principles of Algebraic Geometry by Griffiths and Harris.

Theorems by Pascal and Pappus

The theorems by Pascal and Pappus arise as special cases of the Cayley-Bacharach theorem. First, let's look at Pascal's theorem:

If six points points on a conic are connected in such a way that the line segments between them form a hexagon, then the three pairs of lines corresponding to opposite sides of the hexagon intersect in three points that lie on the same line.

Here is a picture in the case where the conic is an ellipse:

The theorem can be derived from the Cayley-Bacharach theorem as follows. Let the six (distinct) points on the conic be \(B_1, \ldots, B_6\) and the intersection points

\begin{align} X_3 = \langle B_1, B_5\rangle \cap \langle B_2, B_4\rangle, \quad X_2 = \langle B_3, B_4\rangle \cap \langle B_1, B_6\rangle, \quad X_1 = \langle B_2, B_6\rangle \cap \langle B_3, B_5\rangle. \label{eq:pascal-intersection-points} \end{align}

Now we consider two cubic curves each of which is the union of three lines:

\begin{align} C_1: \langle B_1, B_5\rangle \cup \langle B_3, B_4\rangle \cup \langle B_2, B_6\rangle, \quad C_2: \langle B_2, B_4\rangle \cup \langle B_1, B_6\rangle \cup \langle B_3, B_5\rangle. \end{align}

The lines belonging to \(C_1\) are shown dashed, while the ones belonging to \(C_2\) are dotted in the figure above. The curves \(C_1\) and \(C_2\) intersect in nine distinct points, namely \(B_1, \ldots, B_6\) aswell as \(X_1\), \(X_2\) and \(X_3\).

To apply Cayley-Bacharach, let the third cubic curve \(D\) be the union of the conic \(C\) and the line \(\langle X_1, X_2\rangle\). Then \(D\) passes through eight of the nine points \(C_1 \cap C_2\), so it must also pass through the last one, \(X_3\). By Bezout's theorem the lines \(\langle B_1, B_5\rangle\) and \(\langle B_2, B_4\rangle\) each intersect the conic \(C\) in two points. Since the \(B_i\) are assumed to be distinct, none of these intersection points is \(X_3\), so \(X_3\) has to lie on the other component of \(D\) which is the line \(\langle X_1, X_2\rangle\).

The hexagon theorem by Pappus is in turn a special case of Pascal's theorem where the conic is taken to be the union of two lines:

Let \(\ell_1\) and \(\ell_2\) be two lines in the plane. Let \(B_1\), \(B_2\) and \(B_3\) be three distinct points on \(\ell_1\) and \(B_4\), \(B_5\) and \(B_6\) be three distinct points on \(\ell_2\) (all distinct from the intersection point of \(\ell_1\) and \(\ell_2\)). Let the points \(X_1\), \(X_2\) and \(X_3\) be given as in equation \eqref{eq:pascal-intersection-points} as the intersection points of opposite sides of the hexagon \(B_1 B_5 B_3 B_4 B_2 B_6\). Then \(X_1\), \(X_2\) and \(X_3\) are collinear.

The proof is exactly the same specialization of the Cayley-Bacharach theorem as for Pascal's theorem. Here is an illustration of the Pappus configuration:

Associativity of the group law on a cubic curve

Group law on a cubic curve

On a cubic curve in the plane, a group law can be defined as follows. Let \(P\) and \(Q\) be points on the curve \(C\) and consider the line \(\langle P, Q\rangle\) through them. By Bezout's theorem this line intersects \(C\) in one more point which we call \(PQ\).

This gives us a law of composition between two points on \(C\), but the curve equipped with this composition does not form a group yet. There is for example no identity element: If we want \(P\) to be equal to \(PP\), we should look at the tangent line to \(C\) at the point \(P\). This line will meet the curve in one more point, but this third point will be different for each starting point \(P\).

To obtain a group law, we have to chose a point \(O\) on the curve which will act as the identity element. Then we define \(P + Q\) as the third point of intersection of the line \(\langle PQ, O\rangle\) with \(C\). We then have \(P + O = O + P = P\) for all points \(P\) on the curve.

The inverse of \(P\) is constructed by drawing a tangent line to \(O\). This line intersects \(C\) in the third point \(OO\). The point \(-P\) is the third point of intersection of the line \(\langle OO, P\rangle\) with \(C\).

As the line through \(P\) and \(Q\) is the same as the line through \(Q\) and \(P\), the group law is commutative.

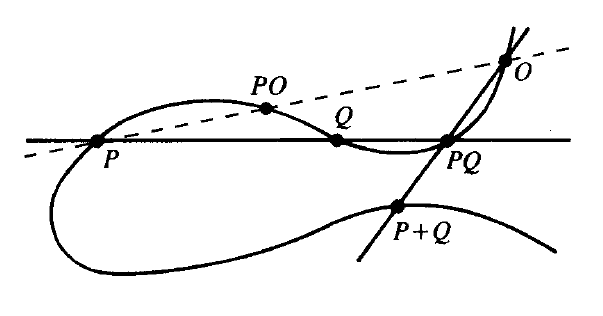
Figure 1: Group law on the elliptic curve (taken from Husemöller)

Associativity from Cayley-Bacharach

The theorem by Cayley-Bacharach can be used to prove the associativity of the group law on a cubic curve. We want to show that for arbitrary points \(P\), \(Q\) and \(R\) on the curve \(C\) it holds that \((P + Q) + R = P + (Q + R)\) where the addition is the group law we just described.

Consider the following two cubic curves each of which is the union of three lines:

\begin{align} C_1: \langle P, Q\rangle \cup \langle R, P + Q\rangle \cup \langle QR, Q + R\rangle, \quad C_2: \langle Q, R\rangle \cup \langle P, Q + R\rangle \cup \langle PQ, P + Q\rangle. \end{align}

The curves \(C_1\) and \(C_2\) have the following eight points in common:

\begin{align} P,\, Q,\, R,\, PQ,\, QR,\, P + Q,\, Q + R,\, O. \end{align}

Moreover, \(C_1\) intersects \(C\) in one more point, namely \((P + Q)R\). Simillarly, \(C_2\) intersects \(C\) in the point \(P(Q + R)\).

This means that \(C_1\) and \(C\) intersect in nine points and since \(C_2\) already passes through eight of them, it also has to pass through the last one, \((P + Q)R\). But there is only one more point of intersection between \(C_2\) and \(C\), so

\begin{align} P(Q + R) = (P + Q)R. \end{align}

The point \(P + (Q + R) = (P + Q) + R\) is then the point of intersection of the line through this last point and \(O\). The following picture illustrates the situation.

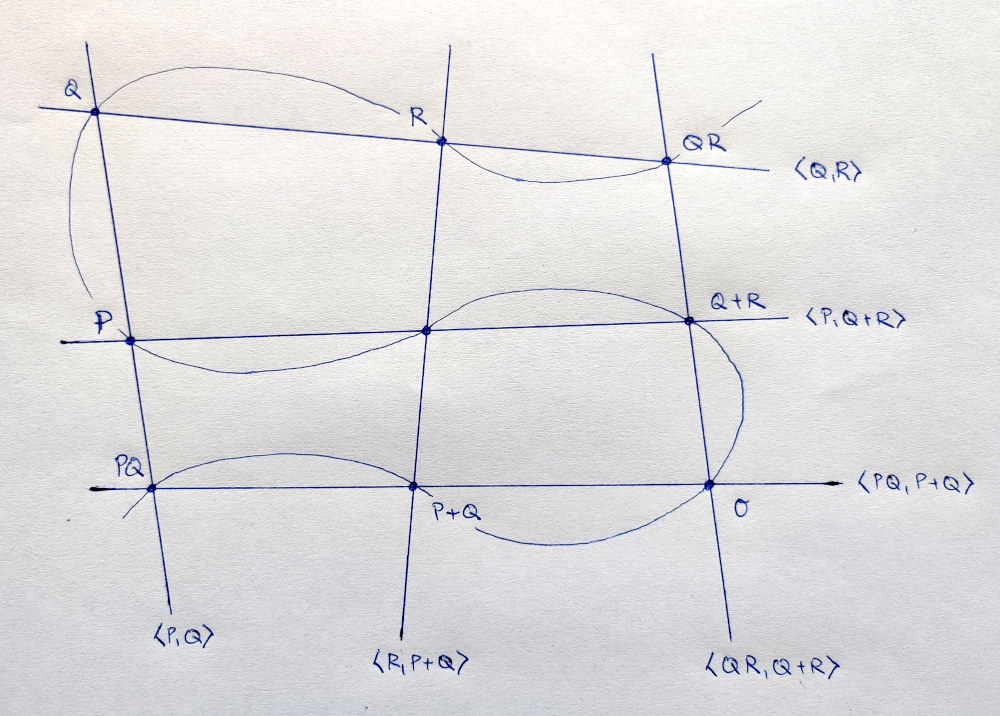
Figure 2: Cayley-Bacharach theorem

References

Joseph H. Silverman, John Tate: Rational Points on Elliptic Curves
Dale Husemöller: Elliptic Curves
David Eisenbud, Mark Green, Joe Harris: Cayley-Bacharach Theorems and Conjectures
Phillip Griffiths, Joseph Harris: Principles of Algebraic Geometry