Generating necklaces
Table of Contents
What are necklaces
A necklace is a sequence of beads on a string. It does not have a beginning or an end and is invariant under rotations. Here is a picture of a drawing of something that resembles a necklace:
Figure 1: A necklace of length 10 with 3 different kinds of beads
Some definitions
Mathematically, a necklace is an equivalence class of strings under rotation. More formally, given an alphabet \(\Sigma_k\) with \(k\) elements (different kind of beads), the set \(\Sigma_k^n\) is the set of all strings of length \(n\) composed of the letters in \(\Sigma_k\). On \(\Sigma_k^n\) we can define an equivalence relation by saying that two strings \(\alpha\) and \(\beta\) are equivalent, \(\alpha \sim \beta\), if they differ by a rotation. A necklace of length \(n\) is an equivalence class of this relation.
On \(\Sigma_k^n\) we also have an order, the lexicographic order \(\leq\) of strings. We use this to pick as a representative for each equivalence class the lexicographically smallest member. We can then write the set of all necklaces of length \(n\) composed of \(k\) letters as
\begin{align} N_k(n) = \left\{\alpha \in \Sigma_k^n \,:\, \alpha \leq \beta \; \text{for all} \; \beta \sim \alpha\right\}. \end{align}Since the alphabet \(\Sigma_k\) is finite we can identify it with the numbers from \(0\) to \(k - 1\).
Here are some examples:
\begin{align} N_2(4) &= \left\{0000, 0001, 0011, 0101, 0111, 1111\right\}, \\ N_3(3) &= \left\{000, 001, 002, 011, 012, 021, 022, 111, 112, 122, 222\right\}. \end{align}Note that \(0010 \in N_2(4)\) is in the same equivalence class as \(0001\), but we pick the latter because it is lexicographically smaller. Similarly, \(020\) is not in \(N_3(3)\), because its rotation \(002\) is smaller.
There are two related notions. The first are Lyndon words. A Lyndon word is an aperiodic necklace. In the example of \(N_2(4)\) the strings \(0001\), \(0011\) and \(0111\) are Lyndon words, but \(0101\) is not because it is periodic.
The second related notion are prenecklaces. A prenecklace is the prefix of some longer necklace. In other words, a prenecklace \(\alpha\) can be extended to a necklace of higher length by appending some other string \(\beta\) to it. The set of prenecklaces of length \(n\) over an alphabet of size \(k\) is denoted \(P_k(n)\).
Some useful results
We would like to have a function \(\operatorname{succ} : P_k(n) \to P_k(n)\) which given a prenecklace of length \(n\) produces the next prenecklace of the same length in lexicographic order. The claim is that the following function achieves this:
Let \(\alpha = u_1 u_2 \cdots u_n \in P_k(n)\) be a prenecklace of length \(n\) and define
\begin{align} \operatorname{succ}(\alpha) = \left[u_1 \cdots u_{i-1} (u_i + 1)\right]^q u_1 \cdots u_j, \end{align}where \(i\) is largest index such that \(u_i < k - 1\),
\begin{align} i = \max \left\{\ell : u_\ell < k - 1\right\}, \end{align}and the integers \(q\) and \(j\) are such that \(q i + j = n\) and \(j < i\).
A proof of this claim can be found in the papers by Fredricksen and Kessler and Fredricksen and Maiorana.
Consider for example an alphabet of size \(k = 2\) and the string \(\alpha = 00111\). For this \(\alpha\) we have \(i = 2\), \(j = 1\) and \(q = 2\), so
\begin{align} \operatorname{succ}(00111) = \left[0 (0 + 1)\right]^2 0 = 01010. \end{align}Note that the definition of the function looks more complicated than it is in practice: Once we have determined \(i\) we can compute \(\operatorname{succ}(\alpha)\) by increasing the letter \(u_i\) and then copying the part of the word until \(i\) repeatedly until we reach a word of length \(n\). This will be the iterative algorithm discussed below.
Another useful function will be the following: For any string \(\alpha = u_1 u_2 \cdots u_n\) of length \(n\), define the function \(\operatorname{lyn}(\alpha)\) as
\begin{align} \operatorname{lyn}(u_1 u_2 \cdots u_n) = \max \left\{p : u_1 u_2 \cdots u_p \; \text{is a Lyndon word} \;\right\}. \end{align}In other words, \(\operatorname{lyn}(\alpha)\) is the length of the longest prefix of \(\alpha\) that is a Lyndon word. Here are some examples:
\begin{align} \operatorname{lyn}(0001) = 4, \quad \operatorname{lyn}(0101) = 2, \quad \operatorname{lyn}(0010) = 3, \quad \end{align}One application of this function is that it gives a criterion for determining if a given string is a prenecklace:
Let \(\alpha = u_1 u_2 \cdots u_n\) be a string and \(p = \operatorname{lyn}(\alpha)\). Then \(\alpha\) is a prenecklace of length \(n\) if and only if
\begin{align} u_1 = u_{p + 1}, u_2 = u_{p + 2}, \ldots, u_{n - p} = u_{n}. \end{align}
Even more importantly, the prenecklaces of length \(n\) can be described recursively in terms of those of length \(n - 1\). This is the content of what is called the fundamental theorem of necklaces:
Let \(\alpha = u_1 u_2 \cdots u_{n-1} \in P_k(n - 1)\) be a prenecklace of length \(n\) and \(p = \operatorname{lyn}(\alpha)\). The string \(\alpha u_n\) obtained by appending \(u_n\) to \(\alpha\) is a prenecklace of length \(n\) if and only if \(u_{n-p} \leq u_n \leq k - 1\). Moreover,
\begin{align} \operatorname{lyn}(\alpha u_n) = \begin{cases} p & u_n = u_{n - p}, \\ n & u_{n - p} \lt b \leq k - 1\end{cases} \end{align}
This theorem leads to the recursive algorithm for generating necklaces shown below.
The number of necklaces of length \(n\) over an alphabet of size \(k\) is
\begin{align} \left|N_k(n)\right| = \frac{1}{n} \sum_{d | n} \phi(d) k^{\frac{n}{d}}, \label{eq:num-necklaces} \end{align}where \(\phi(d)\) is the Totient function (the number of positive integers less than or equal to \(d\) that are relatively prime to \(d\)) and the sum is over the divisors of the length \(n\).
FKM algorithm
The not-so naive algorithm is CAT (constant amortized time) which means that the computationnal effort is proportional to the number of objects that are generated.
Iterative version
The successor function \(\operatorname{succ}(\alpha)\) for prenecklaces gives rise to an iterative algorithm to generate all prenecklaces of a fixed length \(n\) in lexicographic order. We start with the lexicographically smallest word \(0^n\) that consists of \(n\) zeros. We then apply \(\operatorname{succ}\) to it until we reach the lexicographically largest word \((k - 1)^n\).
It remains to filter out those prenecklaces that are in fact necklaces. It turns out that a prenecklace is a necklace if the integer \(i\) that appears in the definition of \(\operatorname{succ}\) divides the length \(n\), so if \(n \mod i \equiv 0\).
Here is a toy implementation of the iterative algorithm in Python:
from collections.abc import Generator def necklaces_iterative(k: int, n: int) -> Generator: u = [0] * (n + 1) yield u[1:] i = n while i > 0: u[i] += 1 for j in range(1, n - i + 1): u[i + j] = u[j] if n % i == 0: yield u[1:] i = n while u[i] == k - 1: i -= 1
Recursive version
The fundamental theorem leads to a recursive algorithm for generating necklaces of length \(n\) over an alphabet of size \(k\). Given a prenecklace \(u_1 \cdots u_{t-1}\) of length \(t - 1\) with \(\operatorname{lyn}(u_1 \cdots u_{t-1}) = p\) we form new strings by appending each of the allowed values between \(u_{n - p}\) and \(k - 1\). The theorem guarantees that these strings are prenecklaces and even tells us what \(\operatorname{lyn}(u_1 \cdots u_{t-1} u_t)\) is.
As before, we are only interested in those prenecklaces that are also necklaces. This happens if \(p\) divides the length \(n\).
Here is the algorithm in Python:
from collections.abc import Generator def necklaces_recursive(k: int, n: int) -> Generator: u = [0] * (n + 1) def gen(t: int, p: int): if t > n: if n % p == 0: yield u[1:] else: u[t] = u[t - p] yield from gen(t + 1, p) for j in range(u[t - p] + 1, k): u[t] = j yield from gen(t + 1, t) return gen(1, 1)
Benchmarks
The algorithm (at least the recursive version) is supposed to have the CAT property which stands for constant amortized time. In the plot below we can see the averge time it took to generate one necklace as a function of the length for an alphabet of size \(k = 2\). One can see that both the iterative and the recursive version reach a plateau.
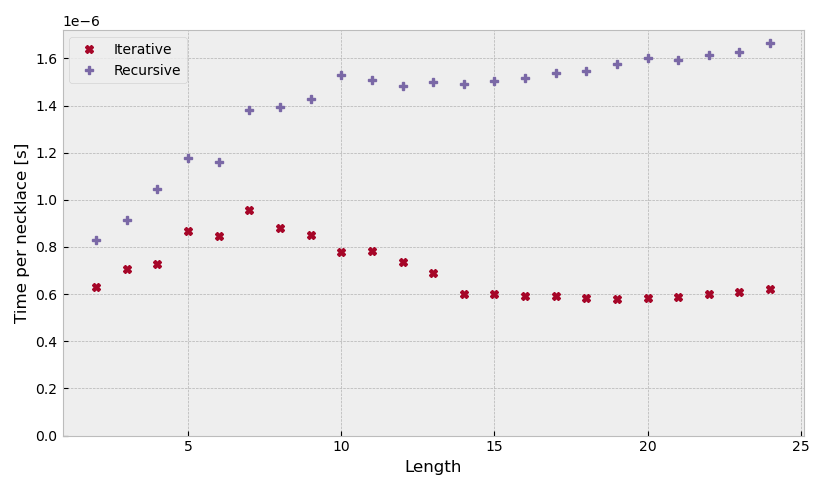
Figure 2: Time per necklace of the FKM algorithm (alphabet of size \(k = 2\))
The time to generate all necklaces of a given length was measured with the timeit module.
To consume the Python generators a deque with maxlen=0 was used as suggested in the recipes section of the itertools module.
This was then divided by the total number of necklaces as computed by equation \eqref{eq:num-necklaces}.
import timeit from collections import deque from collections.abc import Callable from sympy.ntheory import totient, divisors def num_necklaces(k: int, n: int) -> int: return int(sum(totient(d) * k**(n / d) for d in divisors(n)) / n) def time_necklaces(k: int, nmax: int, fun: Callable) -> dict: timings = dict() for n in range(2, nmax): t = timeit.timeit(f"deque({fun.__name__}({k}, {n}), maxlen=0)", globals=globals(), number=100) timings[n] = t / num_necklaces(k, n) / 100 print(fun, n) return timings
Modifications
In the two versions of the algorithm above we are actually generating all prenecklaces and filter out the necklaces by checking if the variables \(i\) (in the iterative case) or \(p\) (in the recursive case) are a divisor of the length \(n\). By simply removing this condition, we can generate all prenecklaces.
It turns out that there are two more modifications that are interesting:
If \(n = p\), the returned necklace is a Lyndon word.
So we can generate all Lyndon words of length \(n\) by changing n % p == 0 to n == p in the recursive version (and simillarly in the iterative version).
If we keep the chec n % p == 0 but instead of returning u[1:] we only return we first \(p\) characters, so u[1:p+1] we are generating De Bruijn sequences.
With fixed content
One might be interested in generating all necklaces where the number of occurrences of each letter from the alphabet is fixed. The set of necklaces over an alphabet of size \(k\) and in which the letter \(i\) appears \(n_i\) times is denoted \(N_k(n_1, \ldots, n_k)\). The length of the necklaces is the sum of the \(n_i\) and the integers \(n_1, \ldots, n_k\) are called the content of the necklace. Here are two examples:
\begin{align} N_2(2, 2) &= \left\{0011, 0101\right\}, \\ N_3(2, 1, 2) &= \left\{00122, 00212, 00221, 01022, 01202, 02021\right\}. \end{align}The number of necklaces with fixed content is
\begin{align} \left|N_k(n_1, \ldots, n_k)\right| = \frac{1}{n} \sum_{d | \operatorname{gcd}(n_1, \ldots, n_k)} \phi(d) \frac{\left(\frac{n}{d}\right)!}{\left(\frac{n_1}{d}\right)! \cdots \left(\frac{n_k}{d}\right)!}, \end{align}where as above \(\phi\) is the Totient function and the sum runs over divisors of the greatest common divisor of the content.
In this paper a simple modifications of the recursive algorithm above can be found that generates all necklaces with fixed content. The idea is to keep track of how many times each letter is still allowed to occur by decrementing \(n_i\) each time the letter \(i\) is used. If \(n_i\) is already zero, the letter \(i\) is skipped.
Here is the algorithm in Python:
from collections.abc import Generator def necklaces_fixed_content(content: tuple) -> Generator: k = len(content) n = sum(content) a = [0] * (n + 1) counts = list(content) def gen(t: int, p: int): if t > n: if n % p == 0: yield a[1:] else: for j in range(a[t - p], k): if counts[j] == 0: continue a[t] = j counts[j] -= 1 if j == a[t - p]: yield from gen(t + 1, p) else: yield from gen(t + 1, t) counts[j] += 1 return gen(1, 1)
According to the paper this algorithm does not have the CAT property, but the paper suggests a modification that does. However, for the purposes that I needed this algorithm for, the above implementation was good enough. The improved algorithm can be found in Figure 4 of this paper and an implementation in C can be downloaded from here.
References
- Harold Fredricksen, Irving J. Kessler: An algorithm for generating necklaces of beads in two colors
- Harold Fredricksen, James Maiorana: Necklaces of beads in k colors and k-ary de Bruijn sequences
- Kevin Cattell, Frank Ruskey, Jow Swada, Micaela Serra, C. Robert Miers: Fast Algorithms to Generate Necklaces, Unlabeled Necklaces, and Irreducible Polynomials over GF(2)
- Joe Swada: A fast algorithm to generate necklaces with fixed content
- The Combinatorial Object Server: combos.org/necklace
- Frank Ruskey: Combinatorial Generation