Ocean waves with WebGL
Table of Contents
Overview
After some time at the sea last summer I wanted to build a simulation of ocean waves. The result can be found here: waves.relint.de. (It does not work well on mobile devices yet, but this might be fixed in the future.)
To get an impression, here is a screenshot:

The simulation is built in WebGL and JavaScript and the code can be found at mvkma/waves (github) or ~mvkma/waves (sourcehut). The goal of this page is to describe some of the ingredients that went into it without going into too much detail. The main source for the physics part of the simulation is the paper Simulating Ocean Water by Jerry Tessendorf. A lof of help came from an implentation of this paper by David Li here: dli/waves (github). This Shadertoy was also very helpful to understand the different light contributions. I did not know a lot about WebGL and shaders before starting this project and learned most of it from webglfundamentals.org.
Physics
The idea is to approximate the height \(h(\vec{x}, t)\) of the ocean surface at position \(\vec{x}\) in the plane and time \(t\) as a Fourier sum,
\begin{align} h(\vec{x}, t) = \sum_{\vec{k}} \hat{h}(\vec{k}, t) \exp(i \vec{k} \cdot \vec{x}). \label{eq:fourier-expansion} \end{align}The sum has \(N^2\) terms with the wave vector \(\vec{k} = (k_x, k_y)\) in the range
\begin{align} -\frac{\pi N}{L} \leq k_x, k_y < \frac{\pi N}{L}. \end{align}The parameter \(L\) is a length scale. In order to ensure that the height field \(h(\vec{x}, t)\) is real, the Fourier modes \(\hat{h}(\vec{k}, t)\) have to satisfy the following reality condition:
\begin{align} \hat{h}^{\star}(\vec{k}, t) = \hat{h}(-\vec{k}, t) \quad \leftrightarrow \quad \operatorname{Im} \left[h(\vec{x}, t)\right] = 0. \label{eq:reality-condition} \end{align}Given initial Fourier modes \(\hat{h}_0(\vec{k})\) at time zero, the modes at time \(t\) are obtained by evolving them in time according to
\begin{align} \hat{h}(\vec{k}, t) = \hat{h}_0(\vec{k}) e^{i \omega_{k} t} + \hat{h}^{\star}_{0}(-\vec{k}) e^{-i \omega_{k} t}. \label{eq:time-evolution} \end{align}The time evolution preserves the reality condition \eqref{eq:reality-condition}. The position-space height field \(h(\vec{x}, t)\) has to satisfy the equation of motion
\begin{align} \frac{\partial^4}{\partial t^4} h(\vec{x}, t) = g^2 \Delta h(\vec{x}, t). \label{eq:eom} \end{align}Here \(\Delta\) is the two-dimensional Laplacian and \(g\) is the gravitational constant. This equation may be derived from the three-dimensional Bernoulli's equations for potential flow by linearization and restriction to two dimensions. We will not go into details here, but a concise derivation can be found in the Tessendorf's paper. In momentum space the equation of motion \eqref{eq:eom} leads to the dispersion relation for the waves:
\begin{align} \omega_k^2 = g k \label{eq:dispersion-relation} \end{align}Our parameters so far are the number of Fourier modes \(N\) and a length scale \(L\) and the question now becomes how to choose the initial Fourier modes \(\hat{h}_0(\vec{k})\). It turns out that the modes \(\hat{h}(\vec{k}, t)\) observed in real ocean waves are well-described by statistical fluctuations with a certain spectrum \(P(\vec{k})\). For wind-driven waves the Phillips spectrum is one such spectrum:
\begin{align} P(\vec{k}) \propto \frac{1}{k^4} \left|\vec{\hat{k}} \cdot \vec{\hat{w}}\right|^2 \exp\left(-\frac{g^2}{k^2 w^4}\right) \exp\left(-k^2 k_0^2\right). \label{eq:phillips-spectrum} \end{align}Here \(\vec{w}\) is a vector that describes the wind, \(k_0\) is a parameter to suppress high-frequency (low-wavelength) waves and the hat on a vector, e.g. \(\vec{\hat{k}}\), denotes a unit vector in the same direction. This leaves us with the following parameters:
- Wind \(\vec{w}\)
- Length scale \(L\)
- Low-wavelength cutoff \(k_0\)
- Gravitational constant \(g\)
- Number of modes \(N\)
Given a choice of parameters and the spectrum \eqref{eq:phillips-spectrum}, Tessendorf suggest to initialize the modes \(\hat{h}_0(\vec{k})\) as
\begin{align} \hat{h}_0(\vec{k}) = \frac{1}{\sqrt{2}} \left(\zeta_0 + i \zeta_1\right) \sqrt{P(\vec{k})}, \label{eq:initial-modes} \end{align}where \(\zeta_0\) and \(\zeta_1\) are two independent random numbers sampled from a Gaussian.
The plot below shows the Phillips spectrum \eqref{eq:phillips-spectrum}. You can play with the parameters to get a feeling for how it changes.
There is one more parameter that is not visible in the spectrum, but affects the look of the waves: the chopping. In reality waves tend to be sharp at the top and flat at the bottom, but those generated by the Fourier sum are more evenly rounded. A way to make the waves appear more choppy is to displace each grid point \(\vec{x}\) at which the height field \(h(\vec{x}, t)\) is sampled by some amount \(\vec{d}(\vec{x}, t)\). This is called the displacement and is also computed by a Fourier sum as
\begin{align} \vec{d}(\vec{x}, t) = -i \alpha \sum_{\vec{k}} \frac{\vec{k}}{k} \tilde{h}(\vec{k}, t) \exp(i \vec{k} \cdot \vec{x}). \label{eq:displacement} \end{align}The parameter \(\alpha\) that scales the displacement determines how choppy the waves look.
Implementation
To implement the wave simulation, the equations from the previous section have to be implemented and the height field \(h(\vec{x}, t)\) has to be drawn to a canvas. The basic steps are:
- Initalize the Fourier modes \(\hat{h}_0(\vec{k})\) according to equation \eqref{eq:initial-modes}
- Ensure that the modes fulfill the reality condition \eqref{eq:reality-condition}
- Evolve the modes to time \(t\) using \eqref{eq:time-evolution} with dispersion relation \eqref{eq:dispersion-relation}
- Evaluate the Fourier sum \eqref{eq:fourier-expansion} by a Fast Fourier Transform (FFT)
- Displace each grid point \(\vec{x}\) by the displacement \label{eq:displacement}, project the height field \(h(\vec{x}, t)\) into the plane and color with some lighting model
The last step takes into account how light from the sky or the sun interacts with the water surface by reflection. There is a lot of physics hidden in this step, but we will not go into detail here.
Each step above will be implemented as a WebGL program that runs on the GPU and the final result will be drawn to a browser canvas. We now describe how the data is represented in these programs.
Data
To store the initial modes \(\tilde{h}_0(\vec{k})\) we need a buffer of size \(N \times N\) that we can then evolve in time and transform to position space. In the WebGL programs all the computations happen in fragment shaders, which assign a color to each pixel. The buffer itself is a WebGL texture attached to a WebGL framebuffer that we can render to and sample from inside the WebGL program. Thus we store all out data in the color values of texture pixels.
The color of a pixel has four components: red, blue, green and alpha. As each component is real (stored as a 16-bit float in our case), one buffer can store two two-dimensional complex sequences.
In our case all three sequences (the height field and the displacements) are real after the Fourier transform which allows us to store them in the same buffer. The reason is that the Fourier transform is linear: If we transform \(\hat{h} + i \hat{g}\) with \(\hat{h}\) and \(\hat{g}\) subject to the reality condition \eqref{eq:reality-condition}, then the result is \(h + i g\), i.e. \(h\) and \(g\) can be read off as the real and imaginary part.
Shaders and programs
Each WebGL program corresponding to a step above renders to a framebuffer with an attached texture. The data in this texture serves as the input for the next program in line and is made available to it by passing a reference as a uniform. The last program finally draws something to the canvas.
Here is an overview over the different programs and the flow of data:

Each program consists of a vertex shader and a fragment shader and takes a number of uniforms as input that (e.g. the simulation parameters or the matrices that determine the view).
All except the last program use the same vertex shader that simply draws a rectangle (quad-2d) that fills the entire canvas.
The shaders used in these programs are:
| Shader | Type | Description |
|---|---|---|
quad-2d |
vertex | Draws a rectangle covering the entire canvas |
vertex-3d |
vertex | Draws a vertex at each grid point, displaced according to the displacement map |
wave-init |
fragment | Initializes the wave spectrum |
conjugation |
fragment | Ensures the complex conjugation property of the Fourier modes |
time |
fragment | Evolves the Fourier modes in time |
fft |
fragment | Calculates a sub-transform step of the Stockham FFT |
normal |
fragment | Determines normals for surface elements |
ocean |
fragment | Computes color of surface elements |
The wave-init, conjugation and time shaders implement the initialization of the Fourier modes, the conjugation property and the time evolution.
The FFT fragment shader fft computes a two-dimensional FFT of the input texture.
More precisely, the shader implements one subtransform of the Stockham FFT algorithm which seems to be first mentioned in this paper from 1967.
A shorter description with some code for a fragment shader can be found here.
I did not spend a lot of time investigating whether the Stockham algorithm is really the best one for this purpose, I simply chose it because it was the one that David Li was using here and because it seemed to perform well enough.
For the interaction with light (e.g. reflection of the sky and the sun) the height field \(h(\vec{x}, t)\) is not enough, we also need the normal vector at each point.
They could be computed as the gradient of the height field and would also be given by a Fourier sum as in \eqref{eq:fourier-expansion}, but this would require us to store and transform two additional real sequences for which there is not enough space in our buffers.
Instead, in the normal shader, a normal at each grid point is computed by taking cross products with vectors to neighboring grid point after the displacement.
Consider the following picture:
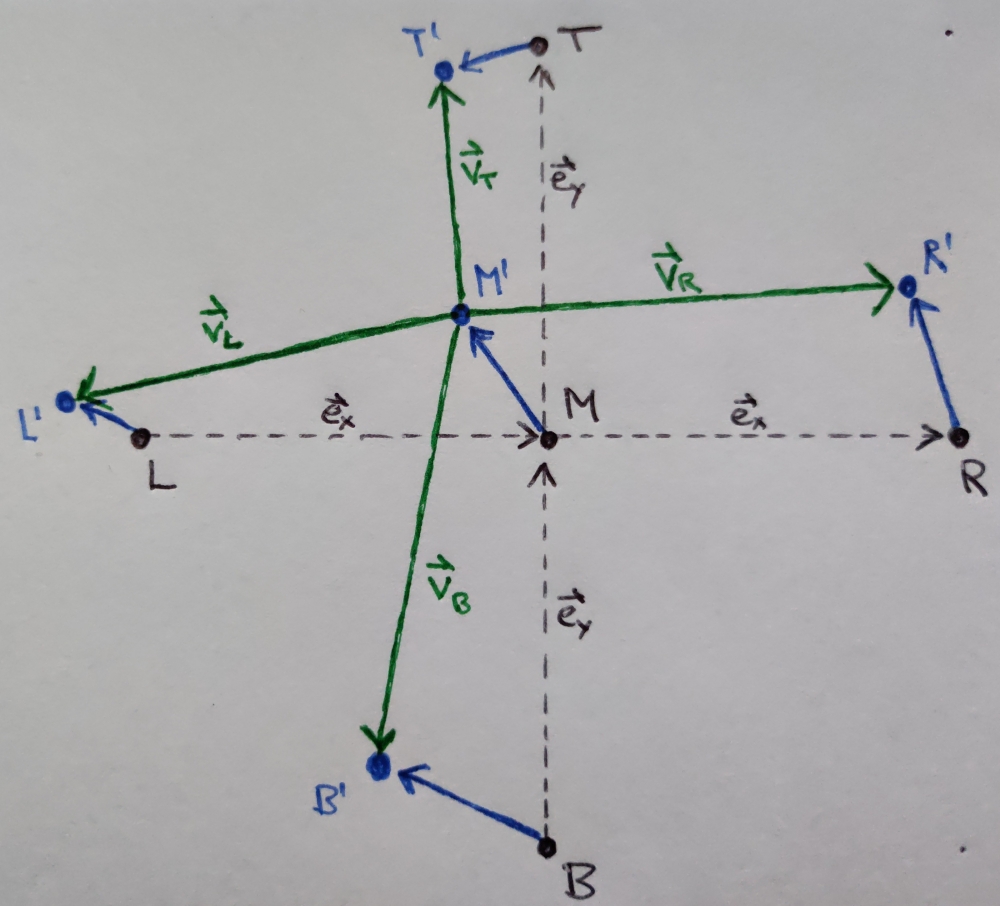
Here \(M\), \(L\), \(R\), \(T\) and \(B\) are grid points at which we sample the height field \(h(\vec{x}, t)\). They are displaced by \(h(\vec{x}, t)\) in \(z\)-direction and by the displacement \eqref{eq:displacement} in the plane. This is shown in blue and the resulting points are called \(M'\), \(L'\), \(R'\), \(T'\) and \(B'\). The vectors drawn in green pointing from \(M'\) to the neighboring displaced grid points are
\begin{align} \vec{v}_L = \vec{b}_L - \vec{b}_M - \vec{e}_x, \quad \vec{v}_R = \vec{b}_R - \vec{b}_M + \vec{e}_x, \quad \vec{v}_T = \vec{b}_R - \vec{b}_M + \vec{e}_y, \quad \vec{v}_B = \vec{b}_B - \vec{b}_M - \vec{e}_y, \end{align}with \(\vec{b}(\vec{x}, t) = (\vec{d}(\vec{x}, t), h(\vec{x}, t))\) and \(\vec{e}_x\) and \(\vec{e}_y\) vectors that point to the next grid point in \(x\)- and \(y\)-direction respectively. The cross product of two of vectors is a vector perpendicular to both of them and the normal at \(M\) is then taken as the average of the four upward-facing normals,
\begin{align} \vec{n}_M = \frac{1}{4} \left(\vec{v}_{R} \times \vec{v}_{T} + \vec{v}_{T} \times \vec{v}_{L} + \vec{v}_{L} \times \vec{v}_{B} + \vec{v}_{B} \times \vec{v}_{R}\right). \end{align}
Finally, the vertex-3d shader puts a vertex at each grid point \(\vec{x}\) displaced by \(\vec{d}(\vec{x}, t)\) and height \(h(\vec{x}, t)\) and projected onto the plane by a perspective projection.
It also picks out the normal at that grid point from the normal map computed by the normal shader and passes it as a varying to the fragment shader.
This is needed by the final ocean fragment shader which implements the reflection of the sky according to Fresnel and the sun.
Outlook
Many more features could be added to the wave simulation, for example:
- Proper sky: Right now, the sky is filled with a slight gradient that starts from the chosen sky color and becomes brighter towards the bottom of the canvas. Ideally, the sky would get brighter towards the horizon and we would also draw the sun. This would require it to take into account the projection and the view which is currently not the case. One could also add a more realistic skybox with pictures of a real sky with clouds.
- Ocean depth as parameter: The dispersion relation \eqref{eq:dispersion-relation} is correct in very deep water. In shallow water of depth \(d\), the correct dispersion relation is \(\omega_k^2 = g k \tanh(k d)\). To simulate waves near the beach where the depth varies the dispersion relation would have to depend on the position, so the FFT is not immediately applicable.
- Interaction with objects or even the shore: Tessendorf's paper has a section on interaction with objects floating in the water. It would also be very cool (but potentially very hard) to simulate the breaking of waves either on the beach or on cliffs.
- Better navigation, controls and support for mobile: I did not spend a lot of time tweaking the controls, so they are a bit rudimentary, especially on mobile.
- Changing the simulation parameters resets the Fourier modes \(\hat{h}_0(\vec{k})\) and initializes them again according to equation \eqref{eq:initial-modes}. It would be nice to make this transition more smooth.
References
- Jerry Tessendorf: Simulating Ocean Water
- David Li: Waves
- WebGLFundamentals: webglfundamentals.org
- D. Brandon Lloyd, C. Boyd, N. Govindaraju: Fast Computation of General Fourier Transforms on GPUs
- Shadertoy by
alro: https://www.shadertoy.com/view/tdSfWG - Phillips spectrum: https://doi.org/10.1017/S0022112058000550