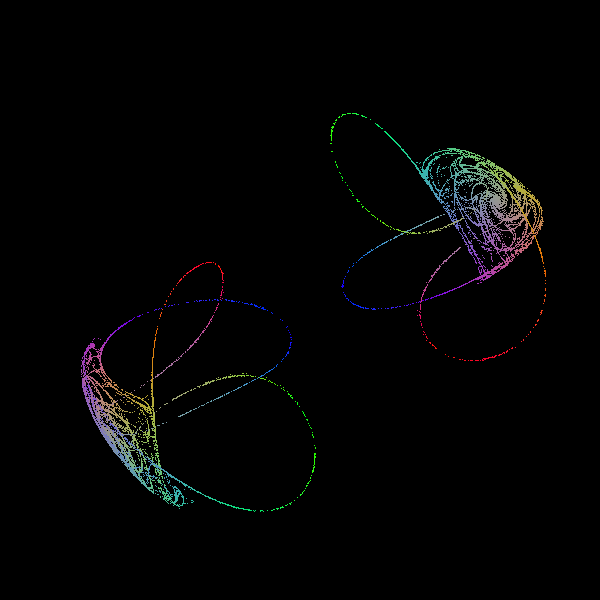Attractors
Table of Contents
Overview
An attractor of a dynamical system is a subset of the phase space that the system evolves to for many initial conditions. Typical examples are fixed points, limit cycles and, geometrically more interesting, strange attractors.
With the tool below the attractors of some simple systems are visualized as particles moving according to the dynamics of the system.
The parameters of the system and some visual parameters can be changed in the text editor components.
They can be set to fixed values or modulated with functions of a global time accessible as time.
The editor should autocomplete the available functions.
To get started, here are some examples. You can click on them and start the visualization with the "start" button.
Ctrl+Enter to apply):Ctrl+Enter to apply):The systems
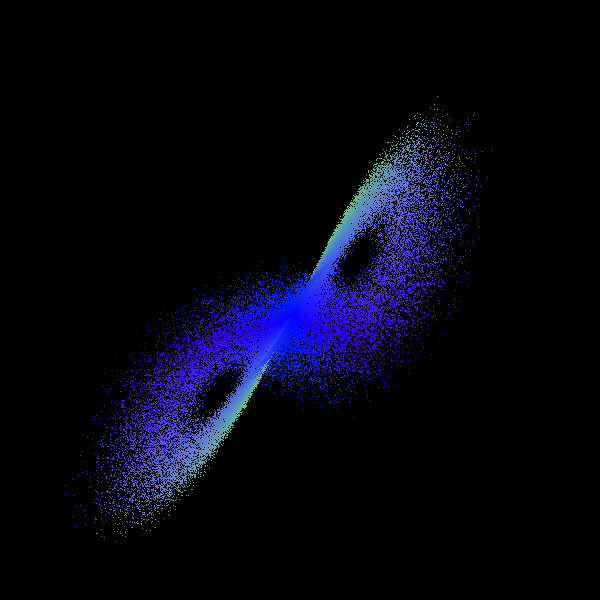
Lorenz system
The time evolution of the Lorenz system is described by the following differential equation:1
\begin{align} \begin{split} \dot{x} &= \sigma (y - x), \\ \dot{y} &= x (\rho - z) - y, \\ \dot{z} &= x y - \beta z. \end{split} \end{align}Here \(\sigma\), \(\rho\) and \(\beta\) are real (positive) parameters.
Edward Lorenz originally studied the system for \(\sigma = 10\), \(\rho = 28\) and \(\beta = \frac{8}{3}\), see here. Keeping \(\sigma\) and \(\beta\) fixed, the system has two non-zero stable fixed points as long as
\begin{align} \rho < \sigma \frac{\sigma + \beta + 3}{\sigma - \beta - 1}. \end{align}For Lorenz' original values of \(\sigma\) and \(\beta\) the critical point where the inequality no longer holds is at \(\rho = \frac{470}{19}\). Varying \(\rho\) slightly around the critical value, we can see how the system changes from being attracted to the fixed points to being repelled by it, see here.
Another interesting point is \(\rho = 99.96\) where the system has knotted periodic orbits, see here.
Rössler system
The equations for the Rössler system are
\begin{align} \begin{split} \dot{x} &= -y - z, \\ \dot{y} &= x + a y, \\ \dot{z} &= b + z (x - c), \end{split} \end{align}with parameters \(a\), \(b\) and \(c\).
Rössler initially (see here) studied the case \(a = 0.2\), \(b = 0.2\), \(c = 5.7\) which can be seen here in the visualization above.
The Rössler attractor is full of periodic orbits and for some values of the parameters all orbits are periodic. For \(a = 0.1\), \(b = 0.1\) and \(c = 8.5\) for instance, the attractors winds around the origin in the \(x\)-\(y\)-plane four times. Here is a case where the parameter \(c\) changes between \(c = 8.5\) and \(c = 9\) every few seconds which shows the transition of the attractors between the periodic and the chaotic behaviour.
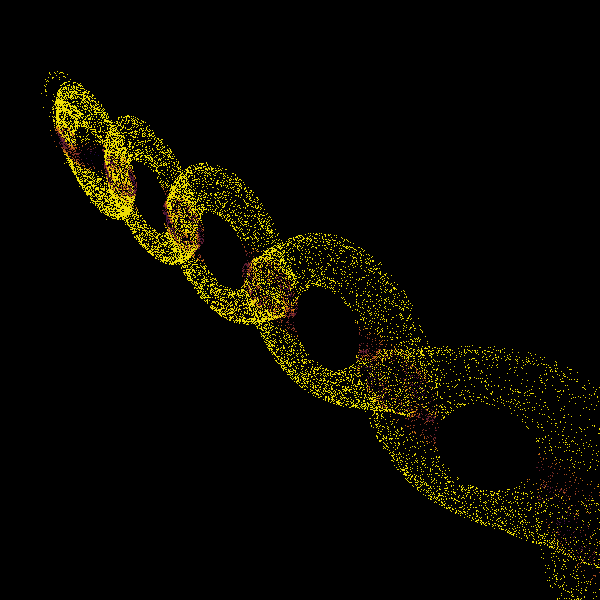
Thomas system
The Thomas system is a cyclically symmetric system described by the system of equations
\begin{align} \begin{split} \dot{x} &= \sin(y) - b x, \\ \dot{y} &= \sin(z) - b y, \\ \dot{z} &= \sin(x) - b z, \end{split} \end{align}with only one parameter \(b\). The original paper also considers and plots some related systems, e.g. one where the \(\sin)\) term is replaced by polynomial.
The critical point at which the system becomes chaotic is \(b \approx 0.208\). Here is the situation just above the critical point (\(b = 0.22\)) and here just below (\(b = 0.18\)).
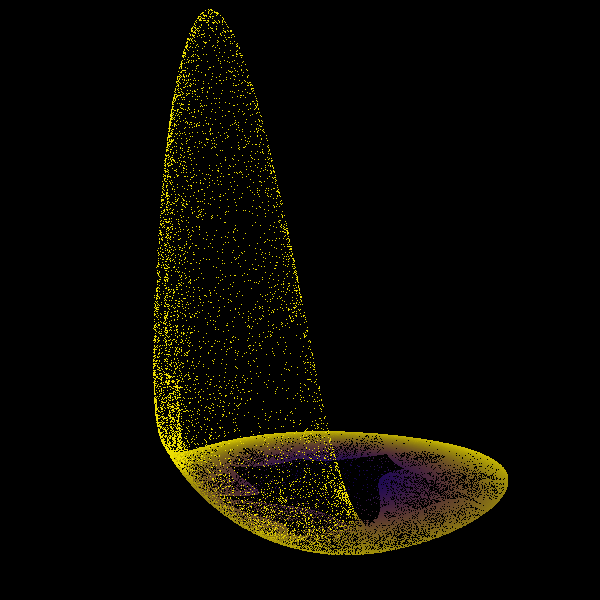
Modified Chua attractor
The modified Chua attractor (see here, section 3.1) is an instance of a multiscroll attractor given by the equations
\begin{align} \begin{split} \dot{x} &= \alpha (y - h), \\ \dot{y} &= x - y + z, \\ \dot{z} &= -\beta y, \end{split} \end{align}where \(h\) is the following combination:
\begin{align} h = \begin{cases} \frac{b \pi}{2 a} (x + 2 a c) & x \leq -2 a c, \\ -b \sin\left(\frac{\pi x}{2 a} + d\right) & -2 a c < x < 2 a c, \\ \frac{b \pi}{2 a} (x - 2 a c) & x \geq 2 a c. \end{cases} \end{align}The parameters of the system are \(\alpha\), \(\beta\), \(a\), \(b\), \(c\) and \(d\).
The parameter \(c\) controls the number of "wheels", see for instance here for the case \(c = 7\).
Van der Pol system
The van der Pol system is a second-order system, but it can be transformed into a first-order two-dimensional system with the following equations:
\begin{align} \begin{split} \dot{x} &= y, \\ \dot{y} &= \mu \left(1 - x^2\right) y - x. \end{split} \end{align}The parameter is \(\mu\). For the visualization the motion is forced to the \(z = 0\) plane with the extra equation \(\dot{z} = -z\).
Here is a visualization of the transition of \(\mu\) from positive to negative values. For positive values we can see a limit cycle. As \(\mu\) decreases and passes zero, a fixed point appears at the center to which the particles spiral.
Implementation
The differential equations above are integrated numerically with the midpoint method with a step size of \(h = 0.001\).
There is a WebGL texture (256 x 256 pixels in size) to store the positions \((x, y, z)\) of the particles, initialized with pseudo-random values in the interval \([-5, 5]\) for each coordinate.
The integration then happens on the GPU in a fragment shader.
Each run of the shader executes a number of integration steps defined by the parameter iterations above.
For the modulation there is a global parameter \(t\) (time in the JSON) that advances by \(\Delta t = 0.05\) on every frame.
The JSON is checked against a schema by the Monaco editor and the value associated to each parameter is transformed into a function that has access to the global time.2
The time resets to zero when the "reset" button is clicked.
Instead of working with the WebGL API directly I decided to use three.js this time. An extra benefit from this are decent default values for the camera and the controls.
Footnotes
Equations (25), (26) and (27) in the the original paper by Lorenz. The paper also contains tables from numerically integrating the equations on an LGP-30 computer. According to the paper "approximately one second per iteration, aside from output time, is required". The calculations were done on the machine by Ellen Fetter.
I would have liked to use CoreMirror instead.
However, I could not find a way to make it work with the JSON schema I was using.
It seems that combining objects with anyOf is not supported at the moment (see this issue in codemirror-json-schema).